Research interests

My research focuses on safety control and networked control systems. My aim is to contribute to the development of mathematical and algorithmic tools for designing controllers that guarantee safety properties of large-scale systems. A key component of my research is the design of resource-aware controllers for networked systems, while ensuring performance and safety specifications.

By combining these areas, I strive to contribute to the development of robust and efficient control tools for the next-generation of cyber-physical systems.

Some of my recent works

Koopman-like Lifted Systems for Correct-by-Design Control

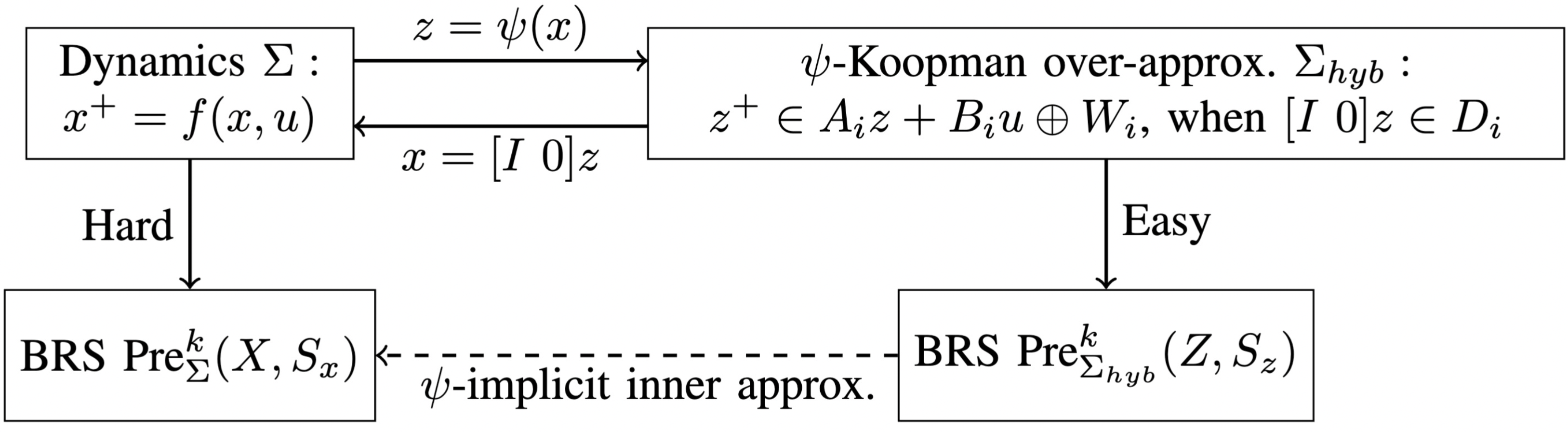
We introduce lifted systems as a generalization of finite-dimensional Koopman approximations to systems with inputs.
A notion of simulation relation is defined between lifted systems. It is proved that this simulation relation implies the containment of both the open- and closed-loop behaviors.
These results enable us to compare different lifting functions and alternative lifted systems in terms of their usefulness in control design.
This simalation relation generalizes (i) hybridizations, (ii) approximate immersions, and (iii) Koopman over-approximations.
Can be used to enforce specifications (or to compute backward reachable sets).

Minimum Sensors-to-Actuators Communication

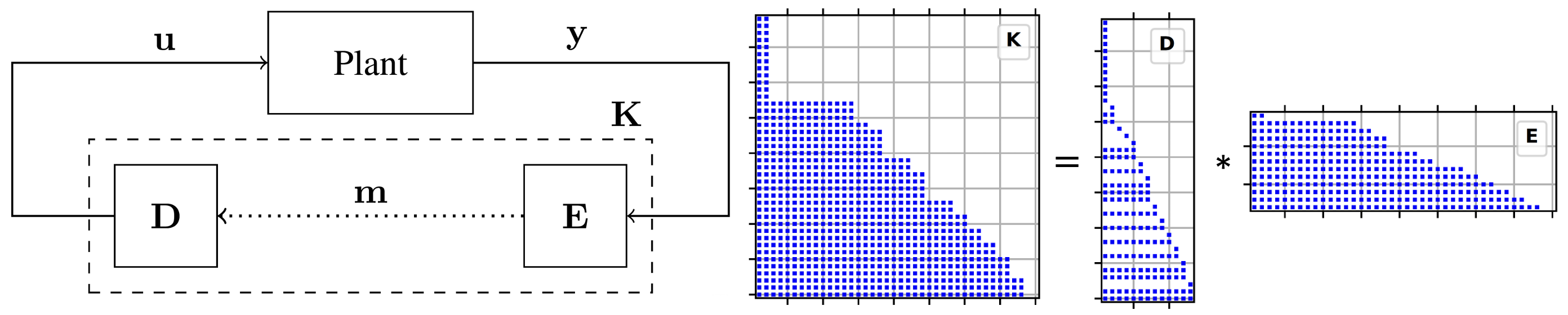
Design a controller that can be implemented with a minimum number of sensor-to-actuator messages, while satisfying safety constraints.
Reduces to a matrix rank minimization problem.
Solution relies on a new matrix factorization that decomposes the controller 𝐊 into an encoder 𝐄 and a decoder 𝐃.

Sparse Sensors and Actuators Activation

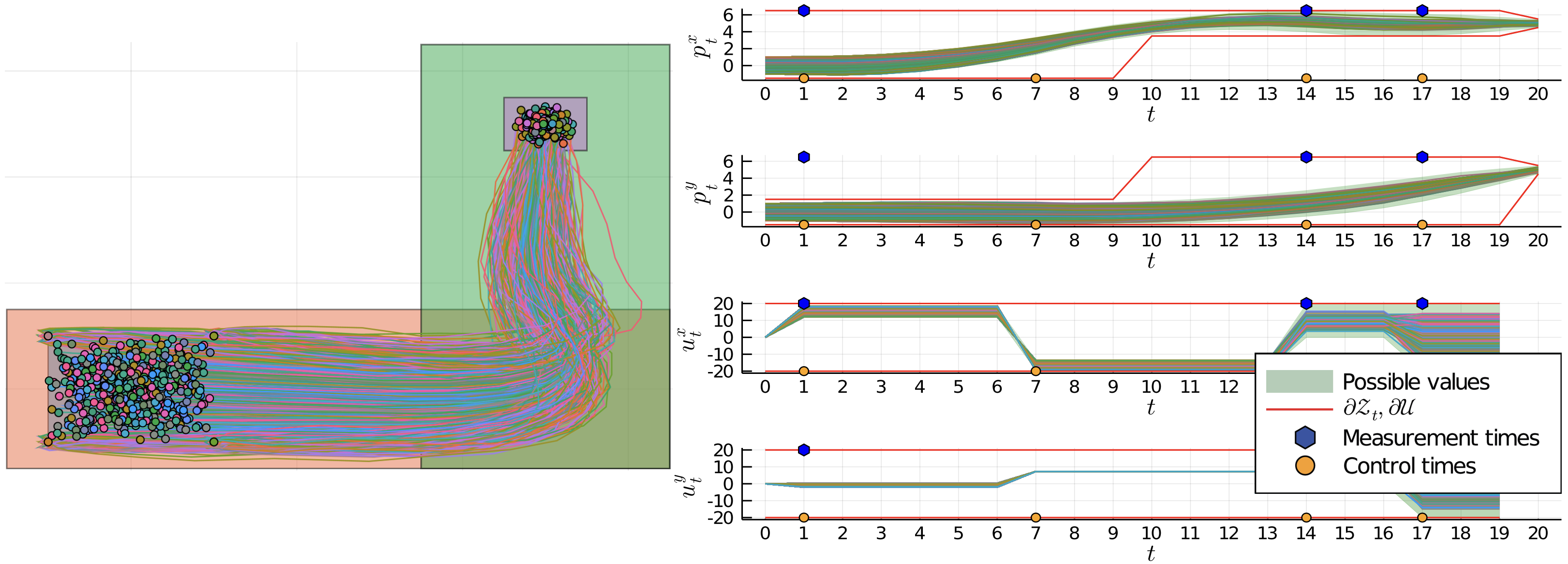
Minimize the use of sensors and actuators, while satisfying safety constraints.
Sensors/actuators sparsity is encoded as a linear constraint. We prove that this constraint remains linear after Youla parameterization.
This leads to a scalable method for sensors/actuators scheduling.

See the paper: Antoine Aspeel, Kwesi Rutledge, Raphaël M Jungers, Benoit Macq, and Necmiye Ozay. Optimal control for linear networked control systems with information transmission constraints.

About my PhD Thesis

My PhD thesis was driven by an applied problem in proton therapy. Essentially, proton therapy aims to destroy tumors using a proton beamline, requiring precise knowledge of the tumor’s position. This becomes challenging with mobile tumors, like lung tumors, which move with the patient’s breathing.

One approach to address this is to use X-ray images of the patient’s chest to measure the tumor’s position. However, X-ray imaging exposes the patient, including healthy tissue, to radiation. Therefore, the number of X-ray images that can be taken is limited.

My thesis tackles the problem of determining the optimal timing for X-ray acquisitions, given a limited budget, to achieve the best tracking of the tumor’s position. From a broader perspective, this problem can be formulated as optimizing the measurement times to obtain the best state estimation of a dynamic system. I studied this problem under different assumptions (linear vs. nonlinear dynamics, expected vs. worst case error).

During my PhD, I had the privilege of collaborating with IBA, the world leader in proton therapy. This collaboration enabled me to bridge the gap between theory and practice by applying my developed methods to the problem of tumor tracking using real medical data.

My PhD thesis Optimal Sampling for State Estimation of Stochastic Dynamical Systems completed under the supervision of Prof. Raphaël Jungers and Prof. Benoît Macq, is available here. The slides of my PhD defense are available here.

Some things I like (non-exhaustive and unordered list)

Hybrid systems theory
Formal methods
Reachability analysis
Koopman theory
Machine learning
Scenario optimization
Polynomial optimization (sum of squares)
System level synthesis
Youla parameterization
Reinforcement learning (and inverse reinforcement learning)